Что такое метод имитации отжига? Мощный алгоритм оптимизации в деталях

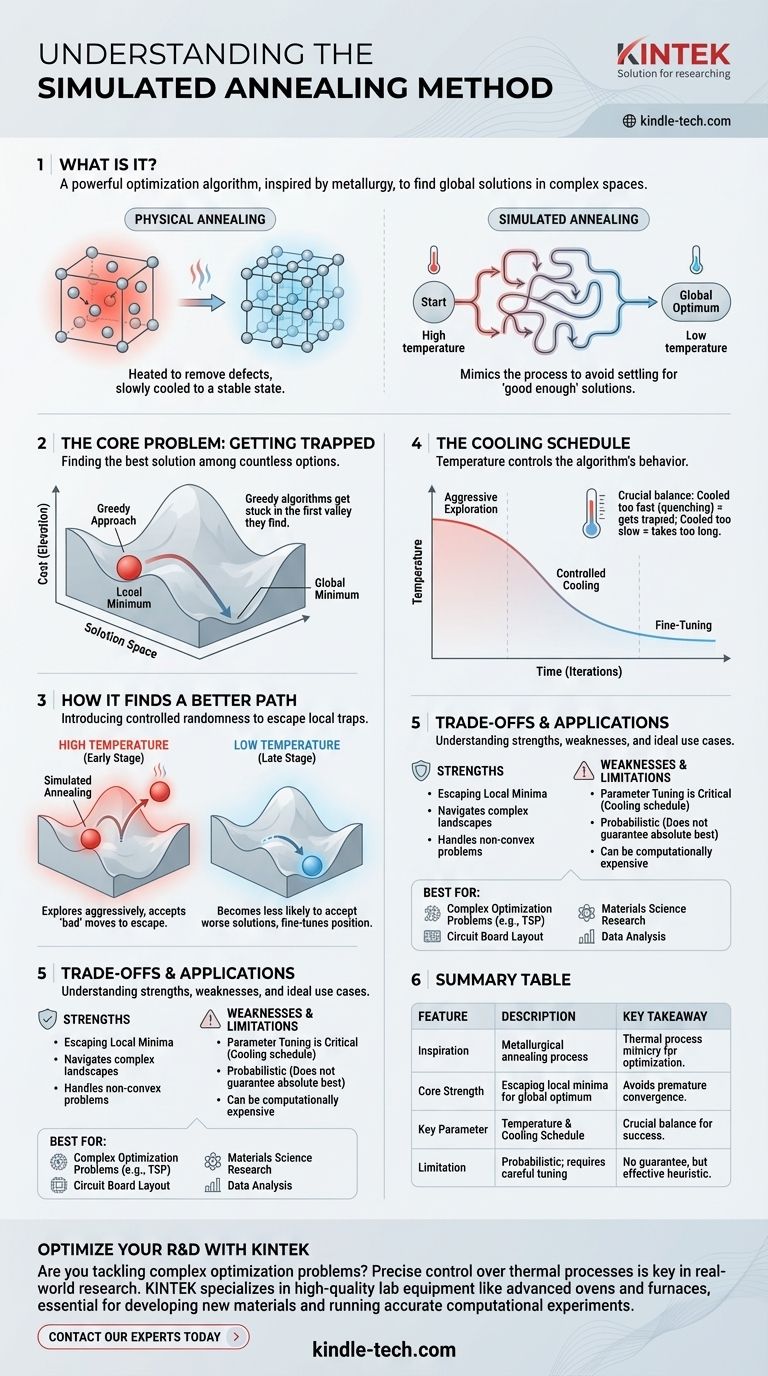
Коротко говоря, имитация отжига — это мощный алгоритм оптимизации, используемый для нахождения хорошего (и часто глобального) решения в обширном и сложном пространстве поиска. Он непосредственно вдохновлен металлургическим процессом отжига, при котором материал нагревается, а затем медленно охлаждается для устранения дефектов и достижения стабильного, низкоэнергетического кристаллического состояния. Алгоритм имитирует этот физический процесс для решения абстрактных вычислительных задач.

По своей сути, имитация отжига позволяет избежать распространенной ловушки, когда приходится довольствоваться «достаточно хорошим» решением, имитируя физический процесс отжига металла. Он начинается с исследования широкого спектра возможностей (высокая температура) и постепенно сужает фокус до высококачественного, стабильного решения (низкая температура).

Основная проблема: попадание в ловушку

Чтобы понять имитацию отжига, вы должны сначала понять проблему, которую она решает: поиск наилучшего возможного решения среди бесчисленных вариантов, задача, известная как оптимизация.

Ландшафт решений

Представьте, что каждое возможное решение вашей проблемы — это точка на обширном, холмистом ландшафте. Высота каждой точки представляет ее «стоимость» — чем ниже высота, тем лучше решение. Ваша цель — найти самую низкую точку на всей карте, глобальный минимум.

«Жадный» подход и его недостаток

Простой алгоритм, часто называемый методом восхождения на холм, начинал бы с случайной точки и всегда двигался бы вниз. Это «жадный» подход, потому что он принимает только те шаги, которые дают немедленное улучшение.

Проблема в том, что этот метод застрянет в первой же найденной долине — локальном минимуме. Он не может знать, существует ли гораздо более глубокая долина, глобальный минимум, сразу за следующим холмом.

Как имитация отжига находит лучший путь

Имитация отжига преодолевает это ограничение, вводя контролируемый элемент случайности, который позволяет ему выходить из этих локальных ловушек.

Вдохновение: физический отжиг

В металлургии нагрев металла дает его атомам достаточно энергии для свободного перемещения, выходя из субоптимальных, дефектных структур. По мере медленного охлаждения металла атомы успевают осесть в высокоупорядоченную, прочную кристаллическую решетку — состояние минимальной энергии.

Алгоритм: температура как регулятор

Имитация отжига использует эту концепцию, вводя параметр температуры. Это не физическая температура, а переменная, которая контролирует поведение алгоритма.

Алгоритм начинается с высокой температуры. В этом состоянии он агрессивно исследует ландшафт решений, подобно энергичным атомам в горячем металле. У него высокая вероятность принятия шагов, которые хуже его текущего положения. Это ключ: совершение «плохого» шага позволяет ему выбраться из локального минимума.

График охлаждения

По мере выполнения алгоритма температура постепенно снижается в соответствии с графиком охлаждения. По мере снижения температуры алгоритм становится все менее и менее склонным принимать худшее решение.

В конце, при очень низкой температуре, алгоритм ведет себя как простой метод восхождения на холм, принимая только улучшения и уточняя свою позицию в том, что, как мы надеемся, является глобальным минимумом.

Понимание компромиссов

Как и любой мощный инструмент, имитация отжига не является универсальным решением. Понимание его ограничений крайне важно для эффективного использования.

Сильная сторона: выход из локальных минимумов

Его основное преимущество — способность перемещаться по сложным, невыпуклым ландшафтам со множеством локальных минимумов. Для задач, где жадные алгоритмы постоянно терпят неудачу, имитация отжига — отличный выбор.

Слабая сторона: критична настройка параметров

Производительность алгоритма очень чувствительна к графику охлаждения. Если охлаждать слишком быстро, он может все равно застрять в локальном минимуме («закалка»). Если охлаждать слишком медленно, поиск решения может занять непрактично много времени. Нахождение правильного графика часто требует экспериментов.

Ограничение: это вероятностный метод

Имитация отжига не гарантирует, что она найдет абсолютно лучшее решение (глобальный минимум). Это эвристика, то есть она предназначена для нахождения очень хорошего решения за разумное время. Всегда существует статистическая вероятность того, что она остановится в субоптимальном состоянии.

Правильный выбор для вашей проблемы

Используйте это руководство, чтобы решить, является ли имитация отжига правильным подходом для вашей задачи оптимизации.

• Если ваша основная цель — решение сложной проблемы со множеством ловушек (локальных минимумов): Имитация отжига — один из лучших инструментов для этой работы, особенно для классических задач, таких как задача коммивояжера или компоновка печатных плат.
• Если ваша основная цель — найти доказуемо оптимальное решение с максимальной скоростью: Сначала вам следует проверить, достаточно ли проста ваша проблема (например, выпуклая), чтобы ее можно было решить более быстрым, детерминированным алгоритмом, таким как линейное программирование или стандартный жадный подход.

В конечном итоге, имитация отжига обеспечивает надежную основу для навигации по обширным и сложным пространствам поиска для нахождения высококачественных решений там, где более простые методы терпят неудачу.

Сводная таблица:

Характеристика	Описание
Вдохновение	Металлургический процесс отжига (нагрев и медленное охлаждение)
Основная сильная сторона	Выход из локальных минимумов для нахождения глобального оптимума
Ключевой параметр	Температура и график охлаждения
Лучше всего подходит для	Сложных задач оптимизации со множеством локальных ловушек
Ограничение	Вероятностный; требует тщательной настройки параметров

Оптимизируйте свои исследования и разработки с KINTEK

Вы решаете сложные задачи оптимизации в материаловедении, химической инженерии или анализе данных? Принципы имитации отжига вдохновлены реальными тепловыми процессами, и точный контроль над этими процессами в вашей лаборатории имеет решающее значение.

KINTEK специализируется на высококачественном лабораторном оборудовании, включая передовые печи и муфельные печи, которые обеспечивают равномерный нагрев и контролируемое охлаждение, необходимые для исследований и разработок. Независимо от того, разрабатываете ли вы новые материалы или проводите вычислительные эксперименты, надежное оборудование является основой точных результатов.

Свяжитесь с нашими экспертами сегодня, чтобы найти идеальное лабораторное решение для улучшения ваших рабочих процессов оптимизации и достижения прорывных результатов.